HoldfasT assessment

Holdfast Analysis:

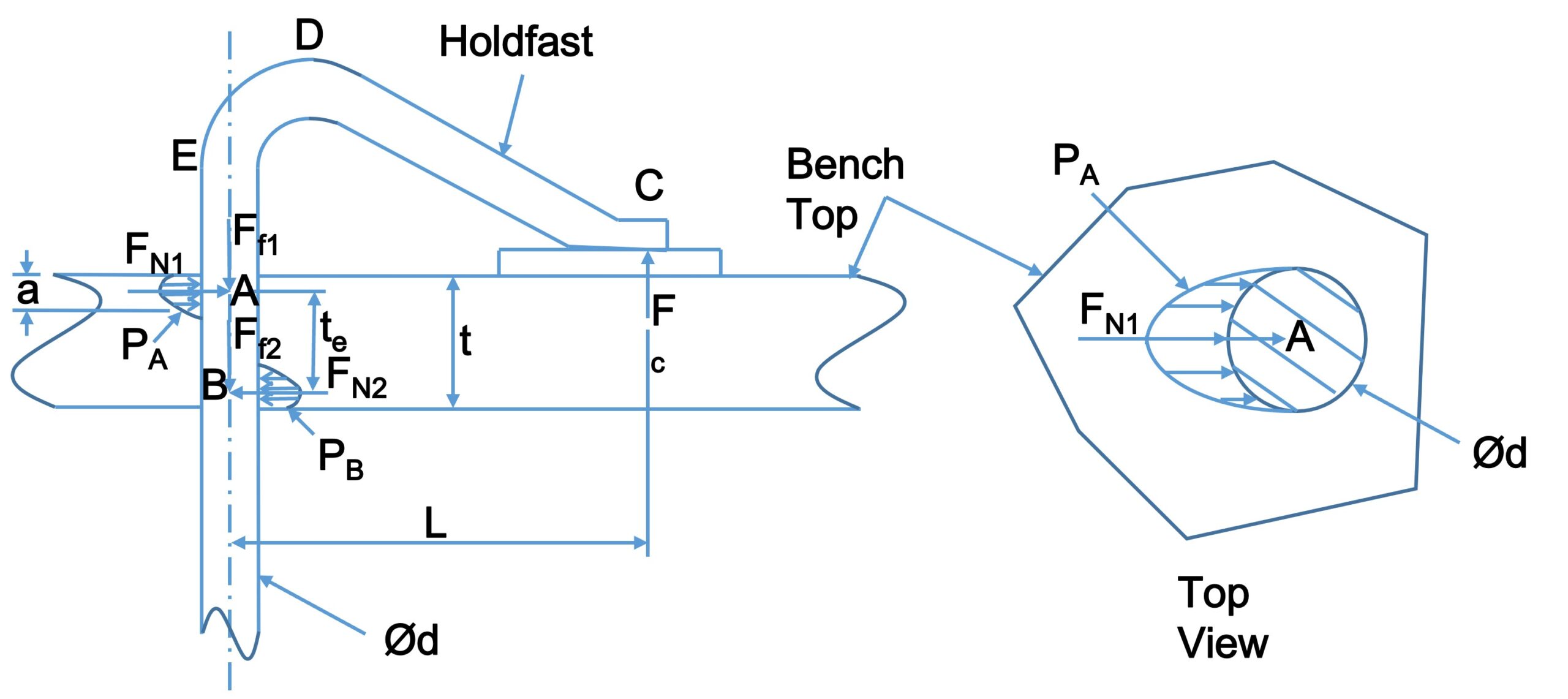
Clamping force development:

Application of a downward force at D results in a resisting force (F_c) at C.  The force at C creates a moment (F_c x L) that is reacted at A and B with pressure loads P_A and P_B.  The pressure loads on the holdfast can be treated as resultant normal forces F_N1 and F_N2.  The two normal forces develop friction loads at A and B (F_f1 and F_f2) that balance out the resulting vertical clamp force at C.

Clamping force relief:

Adequately striking the shaft of the holdfast at E instantaneously relieves or reduces the normal forces at A and B dropping the friction forces below that needed to balance out the clamping force.  The holdfast will tend to slip vertically reducing all of the forces.  More than one relieving strike may be required.

The following is a non-rigorous “ball-park” analysis of a clamped holdfast.

Key assumptions and simplifications:

1) The normal and friction loads are assumed to act through the center of the shaft.

2) The pressure loads (P_A and P_B) are replaced with equivalent normal forces F_N1 and F_N2 acting at a distance t_e apart.

3) Based on hole/shaft fit, top thickness (2.5”) and top material (red oak) that were modeled and assessed, an effective top thickness (t_e) of 2.0” is assumed.

4) As with #2 above, bearing areas of 0.375 in² are assumed (a x d).

5) A friction coefficient (µ) of red oak on steel of 0.49 is assumed (see below).

Clamp Load (F_c):

Informal testing showed that four solid hammer blows at D to various holdfasts consistently firmly seated a test board onto the surface of a digital scale resulting in clamp loads (F_c) of approximately 120 to 140 lb.

Normal forces on the shaft:

The sum of the moments must equal zero, so taking the moments around point A gives:

F_c(L) = F_N2(t_e)

so, letting F_c = 130 lb,   130(6.0) = F_N2(2.0)

therefore,    F_N2 = 390 lb

Likewise summing moments around B gives:

F_N1 = 390 lb

Potential friction forces:

From Engineering toolbox.com and eng.lbl.gov, the static coefficient of friction (µ) for dry cast iron on oak = 0.49.

F_f1 = µ(F_N1)

F_f1 = 0.49(390)

F_f1 = 191 lb

Likewise,

F_f2 = 191 lb

Summing of the forces in the vertical direction gives the actual friction forces:

F_c – F_f1 – F_f2 = 0, 

where F_f1 is assumed to equal F_f2

so,   F_f1 = F_c/2

F_f1 = 130/2

F_f1 = 65 lb

And, F_f2 = 65 lb

(note that F_f1 and F_f2 do not need to be equal)

At 65 lb,  F_f1 and F_f2 are well below the potential friction forces so it can be expected that theholdfast will not slip.

Checking the wood compression stresses (σ_c) at A and B:

σ_c = F_N1/A 

Where the Area   A = a(d) = 0.5(0.75)

A = 0.375”

So,   σ_c = 390/0.375

σ_c = 1040 psi

Note that the compression strength perpendicular to the grain for northern red oak is given as 1010 psi in the US Forest Service’s Wood Handbook (FPL-GTR-113).  Thus, local permanent deformation will likely occur at the A and B locations, especially since the peak stresses will be higher than the calculated value.

Checking the bending (tensile) stress (σ) in the holdfast shaft:

σ = My/I

Where

M (moment) = F_c(L) = 130(6) = 780 lb

y (location) = d/2 = 0.75/2 = 0.375”

I (moment of inertia) = ∏ (d⁴)/64 = ∏ (0.75)⁴/64 = 0.0155

So,   σ = 780(0.375)/0.0155

σ = 18.9 ksi

For A36 mild steel bar the min yield strength is 36 ksi and the ultimate strength is 58 ksi.  Mild steel is a good material choice with its great ductility.  Under hammer blows it will flex and deform without brittle failure.

Holdfasts – Observations and Discussion:

The calculated potential friction forces at A and B (190 lb each) are above that needed to balance the clamping force.  Since the friction forces at A and B are likely not actually equal, it is good that either alone is capable of balancing the full clamping force.  Some references give friction coefficient values for metal on wood varying in the 0.2 to 0.6 range.  For the lower fiction case (µ = 0.2) and the clamp and normal forces kept the same, the potential friction load capability is 78 lb at A and B.  Here the balancing force must be shared between locations A and B.  For the application assessed, if the friction coefficient drops below approximately 0.17 the holdfast can be expected to slip.

It is important to keep the friction coefficient high.  Therefore, the shaft and hole should not be polished, oiled or waxed.  A slipping holdfast might be remedied by cleaning with mineral spirits and/or sanding with coarse grit in a circumferential direction.  Although the analysis showed a lot of margin on the friction load, it is directly dependent on the friction coefficient which can vary greatly based on surface conditions.

As the holdfast’s arm is lengthened, the bending stresses in the shaft and the compressive stresses in the hole increase (for the same clamping force).  Too short of an arm length will result in slippage due to low normal and thereby, friction forces.

Bench top thickness (hole depth) influences the magnitude of the normal forces and hence, the potential friction forces.  The hole depth can also affect the amount of clearance that is needed with the shaft for initial development of the normal forces (binding action).  As the top is thickened and t_e increases, the potential friction forces will trend downward with the clamping force becoming inadequate at some point.  Counterboring the hole from the bottom could remedy this situation.  A longer holdfast arm would also help but the increased bending stresses could drive having to switch to a larger diameter holdfast.  The very high normal forces resulting from too thin of a top would result in substantial bench top fiber crushing and the holdfast being tilted.

Hole-to-holdfast shaft clearance is discussed somewhat above with hole depth.  Thicker bench tops will likely need more hole clearance.  But, in general it is advantageous to have the clearance no more than is needed for the holdfast to work.  This enables greater bearing areas and therefore, less damage to the bench top.

The arm shape (curvature) is likely not critical.  Holdfasts having various arm angles and lengths (including the Type 2 style as referred to elsewhere on this website) were investigated as part of the clamp force testing.  All appeared to clamp securely at around 120 lb with the bench top that was used.

Arm flex or springiness is dependent on the arm’s cross section and length, however, this is likely non-critical for operation. However, springiness might help to lessen compression damage in the hole and to the clamped wood when the hammer blows are applied.  Note that reducing the cross section of the shaft and/or arm to increase flex will increase the bending stresses.  With the assessed 0.75” diameter holdfast the shaft stress is high enough that flexing is occurring.  Additionally, the clamping “foot” of holdfasts are commonly thinned providing some springiness (flex).

Bearing (compressive) stresses in the hole can tend to be on the high side.  It can be expected that at the highest stress points the wood will reversibly compress somewhat allowing the contact area, or bearing area, to increase, thereby redistributing the pressure load and reducing the peak stresses.  When and where the compression stresses exceed the compression strength of the wood, the fibers will permanently crush and deform into a shape that further redistributes the stresses, although the effective hole clearance would increase.  The analysis assumes that some local fiber compressing/crushing occurs thereby shifting the effective load points, hence, an effective top thickness was assessed instead of use of the full bench top thickness when the normal forces were calculated.  In the interest of keeping the analysis simple and avoiding analysis of the actual deformations in the hole, judgment was used in the selection of t_e and a, which are intended to be conservative.

Also on bearing stress and fiber compression, the workbench that this analysis is based upon shows no visible signs of damage at the dog/holdfast holes after many years of holdfast use.  The holes in the bench top were drilled with a 0.75” diameter RJ auger bit (as shown on the workbench construction page) and have minimal clearance with the holdfast shafts.  Lastly, the Wood Handbook indicates that the compression strength of red oak (as with other woods) is substantially higher parallel to the grain than perpendicular to the grain.  Thus, consideration could be given to which way a holdfast is oriented with respect to the grain, especially with wood having low compression strength.

W Bohl, Jan 2018